计算机为何要设计补码,而不是绝对值?
2024-11-07
我之所有有这个疑问,是发现Java中的8字节(32位)的整型long,为什么只能代表$-2^{31}$ ~ $2^{31}-1$?
为什么正数这边要-1呢?不是1个符号位,剩下31个代表数字(取绝对值正反值)就好了?
不过,我的第一个想法是,那么0怎么办?正负0有两个呀,那个才是0呀。
当然,不只我想到的这个问题,还有其他问题,都可以用补码去解决。
符号-绝对值表示法(Sign-Magnitude Representation),在这种表示法中:
- 第一位是符号位:0 表示正数,1 表示负数。
- 后面 31 位表示数值的大小(绝对值)。
这种方法在理论上是可行的,但补码表示法有几个关键的优势,使得它在计算机系统中更适合:
- 简化了加减运算
- 在补码表示法中,加减法的运算可以直接使用硬件电路完成,而不需要区分符号位。
- 补码的表示方法使得负数的加法和减法可以通过简单的加法电路来实现,不需要额外的判断逻辑。
- 例如,用补码表示法时,-1 + 1 可以通过直接相加得到 0,不需要特殊处理符号位。
- 唯一的零表示
- 在符号-绝对值表示法中,0 有两种表示方法:+0(0000...0000)和 -0(1000...0000),这就会导致在比较和判断相等时需要额外的逻辑。
- 补码表示法只有一种零的表示,即 0000...0000,不存在正零和负零的区别,简化了处理。
- 符合二进制溢出的规则
- 补码表示法的正数和负数在二进制中是连续的,循环溢出时会自动变成负数。
- 例如,对于 8 位补码,当最大值 127(01111111)再加 1 时会变成 -128(10000000),自然地回到了负数,符合计算的自然规律。
- 在符号-绝对值表示法中,溢出时会导致符号和数值同时变化,需要额外处理。
- 硬件设计方便
- 补码表示法使得硬件设计更加统一,简化了 ALU(算术逻辑单元)的设计,使加法和减法能够用同一套电路实现。
- 符号-绝对值表示法则需要更复杂的电路来分别处理符号位和数值部分,增加了硬件成本。
结论
虽然符号-绝对值表示法在直观上更简单,但补码表示法的这些优点使得它在计算机系统中成为首选。补码的表示方式不仅有效地解决了符号问题,还简化了计算、硬件设计以及处理逻辑,这也是为什么现代计算机体系结构广泛采用补码的原因。
为什么127+1=-128?
补码的角度
带符号的运算,计算机底层都是用补码来存储的。两者的补码形式如下:
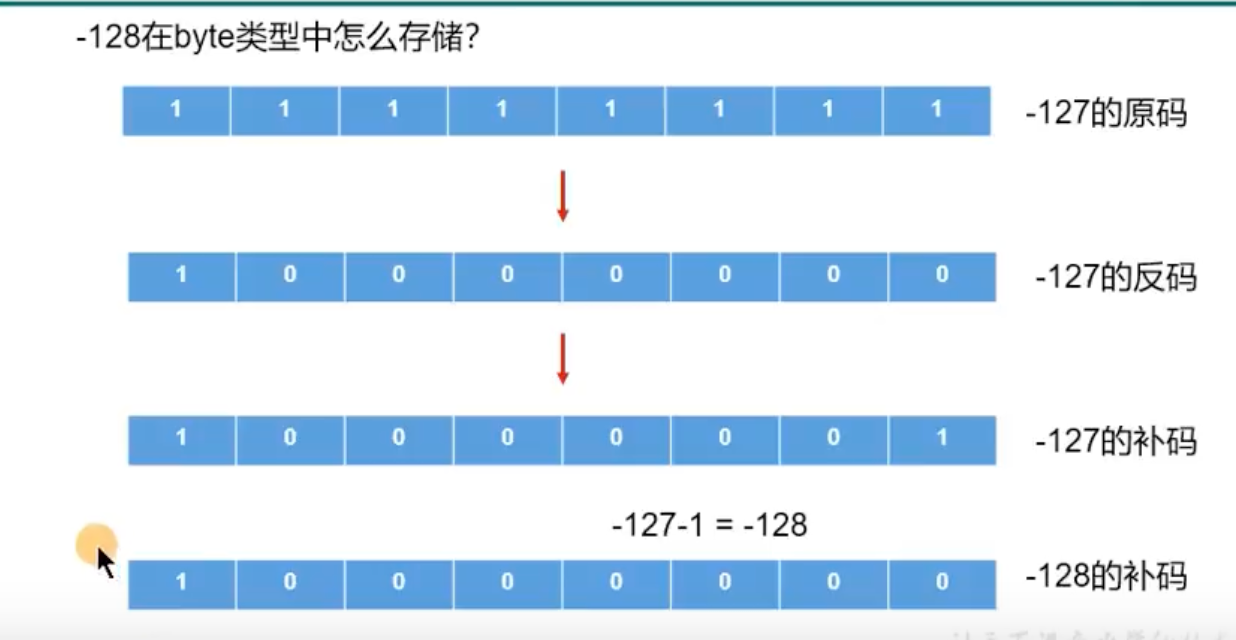
计算的角度
由于01111111是127,127+1是10000000。
以上都是补码。
由于补码的最高位可以参与运算,即又代表符号,又能运算。
因此,
$$ -1\times2^7+0\times2^6+...=-128 $$
补码的快速运算
补码的最高位参与运算。例子:
1001 1001
简单算法
直接计算。
-128 + 16 + 8 + 1 = -103
复杂算法
取反码,再取原码,再转换。
减一得反码
1001 1000
取反得原码
1110 0111
算数
-(64+32+4+2+1)=-103
